Zasada złotego podziału, znana jest już od starożytności i wykorzystywana w przeróżnych dziedzinach, takich jak architektura, malarstwo czy projektowanie. Założenia złotego podziału sprowadzają się do zachowania proporcji między długością dłuższego i krótszego boku prostokąta.

Najprostsza definicja pochodzi z Wikipedii i brzmi:

Zapraszam do obejrzenia bardzo ciekawego filmiku obrazującego zasadę złotego podziału.

Od złotego podziału do liczb Fibonacciego

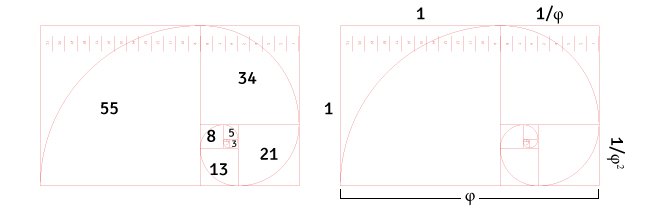
Jak pewnie zauważyliście w prostokącie powyżej umieściłem liczby. W 1202 r. włoski matematyk Leonardo Fibonacci opracował ciąg liczb noszący nazwę Ciągu Fibonacciego. W ciągu tym pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich. Tak więc, 0, 1, 1, 2, 3, 5, 8, 13, 21 itd.

Ciąg liczb Fibonacciego, który został oparty na złotej proporcji można zastosować na przykład przy tworzeniu podstawowej siatki podziału strony. Niemiecki typograf Jan Tschichold opracował szkic strony w formacie octavo (8vo). Przy jej tworzeniu zastosował stosunek 21:34 czyli liczby Ciągu Fibonacciego.

Taką siatkę można otrzymać w bardzo prosty sposób. Ustalamy wielkość początkową naszej siatki, czyli jaki rozmiar będzie mieć nasz bazowy kwadrat. Dla zobrazowania utworzyłem siatkę z kwadratem początkowym 10×10 pikseli.

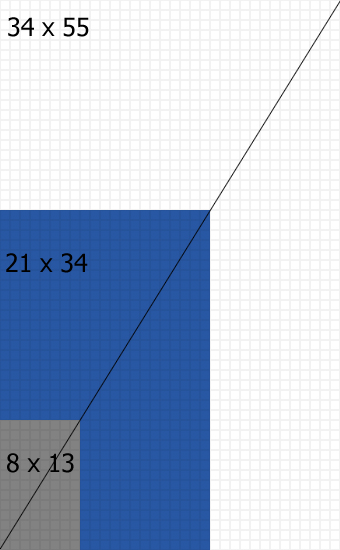
1 +1 = 2, 2+1=3, 3+2=5. Z sumy kwadratów 3 i 5 możemy uzyskać pierwszą siatkę 5+3=8, 8+5=13. Kolejno z 8 i 13 uzyskujemy większą siatkę (szary prostokąt), sumując następne liczby według wzoru Fibonacciego 13+8 =21, 21 + 13 = 34 (niebieski prostokąt) i tak można w nieskończoność. Dzięki czarnej linii możecie zaobserwować jak harmonijnie przyrasta wielkość siatki.

Skoro już mamy siatkę strony trzeba ułożyć blok tekstowy tak by harmonia została zachowana.

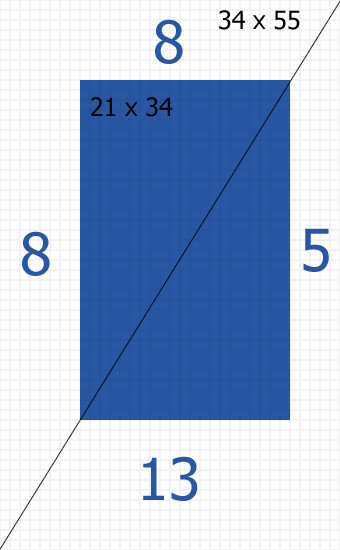
Strona ma rozmiar 34×55 , blok tekstowy 21×34, a czarna linia ciągle obrazuje nam, że nasza harmonia nie została zachwiana. Margines wewnętrzny stanowi sumę 5 kwadratów (1+1=2, 2+1=3, 3+2=5). Margines zewnętrzny i górny sumę 8 kwadratów (1+1 = 2, 2+1=3, 3+2=5, 5+3=8) Margines dolny sumę 13 kwadratów. W oto tak prosty sposób uzyskaliśmy ścisłą i spójną relacje między szerokościami siatki. Możemy również wykonać taki rozkład strony dla rozmiaru 21×34, ale musimy pamiętać, aby zastosować liczby z wcześniejszych sum Fibonaccigo. Dla strony z siatką 21×34 blok tekstowy wyniesie 8×13, margines wewnętrzny 3, zewnętrzny i górny 5, dolny natomiast 8.

Oto jak wygląda ten proces z wypełnionym blokiem tekstowym.

Złoty podział w projektowaniu

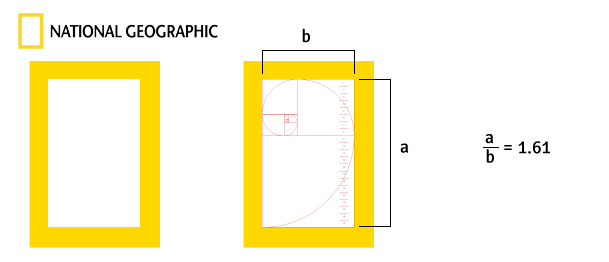
Złoty podział ma szerokie zastosowanie od malarstwa przez architekturę po branding. Złotym podziałem fascynowało się wiele wielkich umysłów. Od czasów Platona po dziś dzień. Najłatwiej zaobserwować go w logo National Geographic.

Złoty podział to nie tylko prostokąty. Pamiętajmy, że chodzi o zachowanie proporcji 1.61 czyli można zastosować go do logo z okręgami, na przykład tak, jak zrobiło to Pepsi.

Pełny brief Pepsi można obejrzeć pod linkiem

Oto kilka wymiarów prostokątów z zachowaniem złotej proporcji jeśli byście chcieli sami zastosować złoty podział we własnych projektach np: wizytówkach, ulotkach.

5 x 8,09 cm, 20 x 32,36 cm, 27 x 43,69 cm, 7 x 11,33 cm, 21 x 33,98 cm, 28 x 45,30 cm, 12 x 19,42 cm, 24 x 38,83 cm, 30 x 48,54 cm, 18 x 29,12 cm, 25 x 40,45 cm, 40 x 64,72 cm.

Podczas tworzenia własnych projektów z zachowaniem złotej proporcji warto skorzystać z dostępnego w Internecie kalkulatora.

Złota proporcja, a webdesign

Pewnie zastanawiacie się czy da się zastosować tą zasadę do projektowania stron WWW? Ależ oczywiście, że się da. Musimy pamiętać, że najczęściej strony są scrollowane w dół więc nasz prostokąt zbudowany ze złotej proporcji musi być ułożony poziomo. Łatwo można się tego nauczyć na przykładzie projektu Design Staff.

W finalnej wersji stylistyka strony wygląda inaczej designstaff.org, ale ciągle została zachowana zasada złotej proporcji.

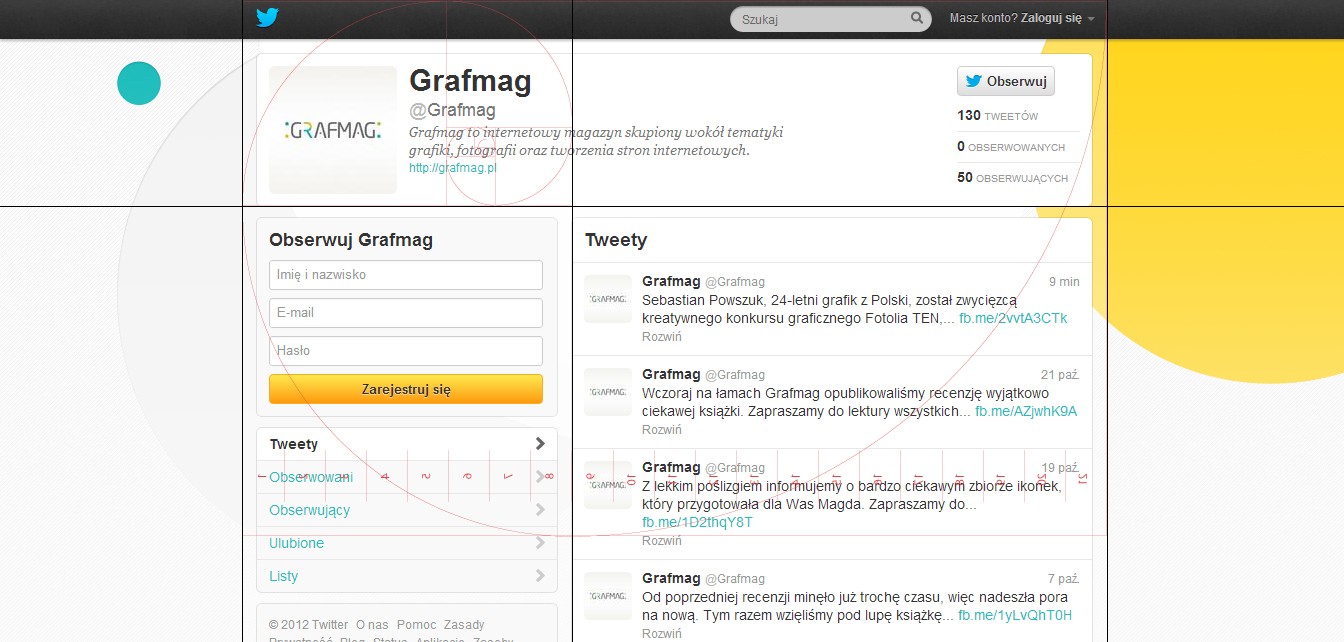
Złoty podział nie jest rozpowszechniony w projektowaniu stron WWW, ale można go spotkać czasem w najmniej spodziewanym miejscu. Najlepszym tego przykładem będzie znany większość portal http://twitter.com

Wzór złotego podziału wykonany w wektorze można pobrać ze strony Adobe